Улучшение тестов для statistics, часть 1
date = fromGregorian 2016 jun 01
category = "Численные методы"
tags = ["численные методы", "тестирование"]
Это первый пост из, как мне кажется, длинной серии о том, как я исправлял тесты к
пакету statistics и находил и
чинил баги в
math-functions. Как и
подобает подобному сочинению, оно состоит большей частью из картинок и
формул.
Тут надо сказать несколько слов похвалы о проекте IHaskell. Отладка численного кода — занятие интерактивное, и один из основных инструментов — рисование графиков. IHaskell делает это относительно удобным. Нотебуки, в которых я отлаживал код, можно найти в репозитории numeric-notebooks.
На данный момент (31 мая 2016 г.) тесты для statistics через раз выдают ложные
срабатывания, а может быть и истинные, отличить их всё равно можно только на
глаз. Проблема в тестировании численного кода состоит в том, что вычисления с
плавающей точкой лишь аппроксимируют вычисления с действительными
числами. Потому, если обычно в тестах можно использовать равенство, то тут
приходится использовать приблизительное равенство, причём «приблизительно» в
каждом случае будет разным.
Для абсолютного большинства действительнозначных функций, в лучшем случае, можно
добиться того, что вычисленное значение функции будет отличаться от истинного не
более чем на
\[f(x) = (-\log x)^{-1/4} \qquad g(x) = \exp( -1/x^4 ) \]
Нетрудно видеть, что \((f \circ g)(x) = x\), однако, если мы построим графики для
\x → x и \x → f (g x), то увидим катастрофу:
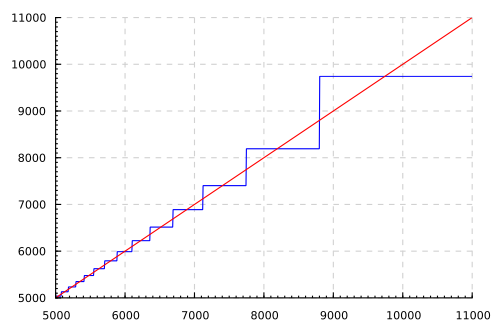
Предоставив читателю шанс подумать о том, откуда взялись катастрофические ошибки
округления, рассмотрим, к чему приводит неизбежная потеря точности при композиции
функций в деле написания тестов. В том случае,если мы хотим просто проверить,
что
Но как только мы хотим написать тест для композиции функций, например \((f^{-1}\circ{}f)(x)\approx{}x\), нам придётся учитывать ошибки округления. Наивный подход состоит в том, чтобы сделать консервативную оценку ошибки, не зависящую от x. Но он не работает: с большой вероятностью найдётся угол в пространстве параметров, где ошибки округления будут хуже, а для большей части параметров оценка будет слишком консервативной. Таким образом мы приходим к необходимости оценки ошибок округления.
Распространение ошибок
Ошибки округления удобнее всего выражать в виде относительных ошибок: \(x(1+\varepsilon)\), так как приключаются они как раз в последних битах мантиссы, и потому всегда составляют некоторую долю числа. Для начала рассмотрим, какой ответ даёт точная функция, которой на вход подано число, заданное с ошибкой. Будем полагать функцию дифференцируемой, и, считая ε малым, ограничимся линейным членом в ряде Тейлора.
\[f\left(x[1+\varepsilon]\right) \approx f(x) + f'(x)\cdot x\varepsilon = f(x)\left[1 + \frac{xf'(x)}{f(x)}\varepsilon\right] \]
Отсюда видно, что относительная ошибка изменяется в \(|xf'(x) / f(x)|\) раз. Пусть теперь у нас есть две функции \(f,g :: \mathbb{R}\rightarrow\mathbb{R}\) и их приближение числами с плавающей точкой: \(\bar{f},\bar{g}\). С этого момента будем обозначать приближённые значения чертой над функцией/значением. Теперь нам надо найти ответ на вопрос, чему равна ошибка округления для \(\bar{g}(\bar{f}(x))\). Введём следующие обозначения:
\[\begin{aligned} y &= f(x) \\ z &= g(y) \\ \end{aligned}\]
Пусть \(x\) является числом, представимым как Double, тогда из-за погрешностей
округления:
\[\bar{y} = \bar{f}(x) = y(1 + \varepsilon_f)\]
Вычислим теперь значение точной функции \(g(\bar{y})\)
\[g(\bar{y}) = g(y)\left[1 + \frac{yg'(y)}{g(y)}\varepsilon_f\right]\]
Но вычисление \(\bar{g}\) само по себе вносит ошибку округления, так что окончательным ответом будет:
\[\bar{g}(\bar{f}(x))=g(y)\left(1+\frac{yg'(y)}{g(y)}\varepsilon_f+\varepsilon_g\right)\]
Теперь мы можем сделать консервативную оценку сверху на относительную погрешность \(\bar{g}(\bar{f}(x))\). Если мы будем считать максимальную ошибку округления для обоих функций одинаковой и равной ε, то
\[\varepsilon_{g\circ{}f} \leq \varepsilon\left[1+\left|\frac{yg'(y)}{g(y)}\right|\right]\]
Это выражение нетрудно обобщить и на композицию большего числа функций, но нам этого не нужно, и мы перейдём к написанию тестов.
Тесты для квантилей
У класса типов для
непрерывных распределений
есть методы
cumulative и
quantile которые являются взаимно
обратными. Потому естественным будет написать тест cumulative . quantile ≈ id.
Кроме того,
density
является производной cumulative, что нам пригодится.
Надо также заметить, что тест удобно писать как раз в виде cumulative . quantile ≈ id, т.к. область определения квантилей — интервал [0,1], а область
определения cumulative меняется от распределения к распределению.
Теперь нам надо написать оценку для ошибки, когда \(g = f^{-1}\):
\[\varepsilon_{f^{-1}\circ{}f} \leq \varepsilon \left[1 + \left|\frac{f(x)(f^{-1})'(y)}{x}\right|\right] \]
Или в виде кода на Хаскелле:
roundtripError :: ContDistr d => d -> Double -> Double
roundtripError d x
= m_epsilon/2 * (1 + abs (y / x * f_inv' y))
where
f = quantile d
f_inv' = density d
y = f xТеперь можно начать строить картинки с оценкой ошибки и фактической ошибкой при
вычислении cumulative . quantile. Первой жертвой будет
бета-распределение, как
первое по алфавиту. Кроме того, QuickCheck каждый раз находит для него
какую-нибудь ошибку. Ниже приведён график для параметров
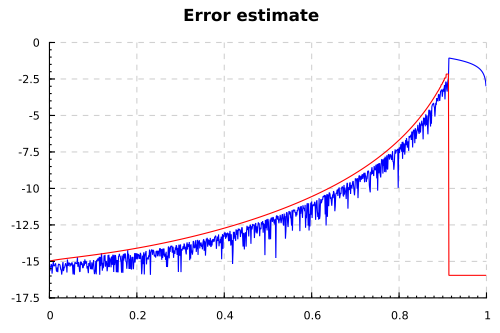
Не надо обращать внимание на полное расхождение ответов при
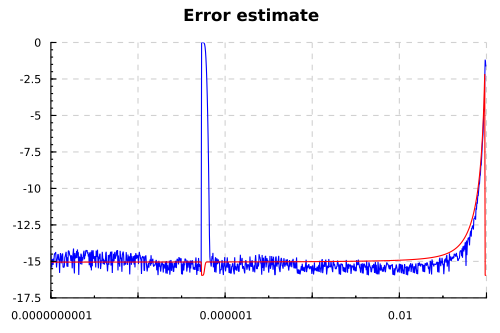
Что мы видим? При малых p функция начинает терять точность, где-то на один
десятичный знак. И ЧТО ЗА КОЛ торчит посредине графика? Запустив тесты несколько
раз, можно наткнуться и на другие ошибки, хотя и менее впечатляющие: например,
для
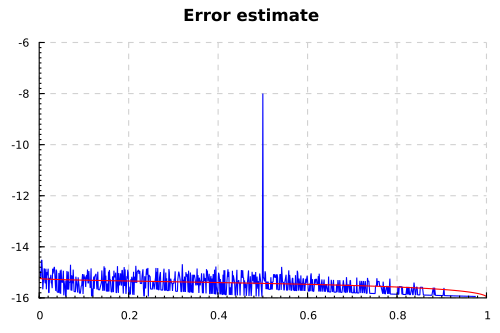
Итого у нас есть работающий метод оценки ошибок округления и баги (если
посмотреть на определения cumulative и quantile) в неполной бета-функции и
обратной неполной бета-функции. Но охота за этими багами — уже другая история.
